当前位置：首页 > 百科 > 儿童教育

二元函数可微的充要条件公式（二元函数全微分存在的充要条件）

来源： 最后更新：22-05-24 03:01:20

　　二元函数可微的充要条件公式是若函数对x和y的偏导数在这点的某一邻域内都存在，且均在这点连续，则该函数在这点可微。必要条件：若函数在某点可微，则函数在该点必连续，该函数在该点对x和y的偏导数必存在。

　　二元函数可微性：

　　定义：

　　设函数z=f(x，y)在点P0(x0，y0)的某邻域内有定义，对这个邻域中的点P(x，y)=(x0+△x，y0+△y)，若函数f在P0点处的增量△z可表示为:

　　△z=f(x0+△x，y+△y)-f(x0，y0)=A△x+B△y+o(ρ)，其中A，B是仅与P0有关的常数，ρ=〔(△x)^2+(△y)^2〕^0.5.o(ρ)是较ρ高阶无穷小量，即当ρ趋于零是o(ρ)/ρ趋于零。则称f在P0点可微。

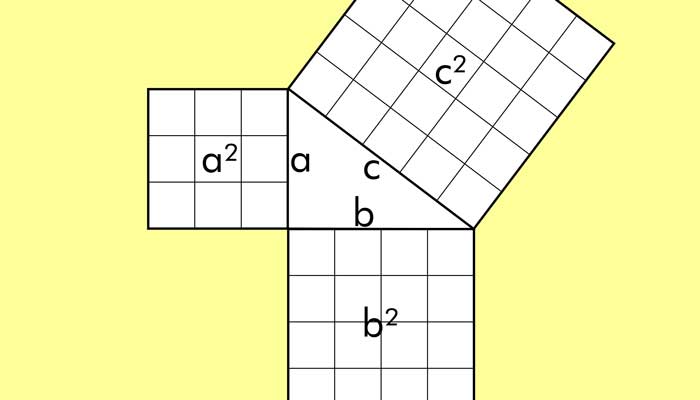
　　可微性的几何意义：

　　可微的充要条件是曲面z=f(x，y)在点P(x0，y0，f(x0，y0))存在不平行于z轴的切平面Π的充要条件是函数f在点P0(x0，y0)可微。

　　这个切面的方程应为Z-z=A(X-x0)+B(Y-y0)。

标签: 充要条件  函数  公式  

免责声明：本文系转载，版权归原作者所有；旨在传递信息，其原创性以及文中陈述文字和内容未经本站证实。

本文地址:http://www.jxyuer.com/baike/jiaoyu/255604.html

牛顿晚年为什么疯了贴吧（牛顿晚年疯了吗）

网站首页 返回栏目

山亭造句（书亭的造句）